[SWEA] #1251 - 하나로

💡 출처
https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AV15StKqAQkCFAYD
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
💡 문제
[설명]
당신은 인도네시아 내의 N개의 섬들을 연결하는 교통시스템 설계 프로젝트인 ‘하나로’를 진행하게 되었습니다.
하나로 프로젝트는 천해의 자연을 가진 인도네시아의 각 섬 간 교통이 원활하지 않아 관광 산업의 발전을 저해하는 요소를 줄이고 부가 가치를 창출하고자 진행하는 프로젝트입니다.
본 프로젝트에서는 인도네시아 내의 모든 섬을 해저터널로 연결하는 것을 목표로 합니다.
해저터널은 반드시 두 섬을 선분으로 연결하며, 두 해저 터널이 교차된다 하더라도 물리적으로는 연결되지 않는 것으로 가정합니다.
아래 그림 1과 같은 경우, A섬에서 D섬으로는 연결되었지만 A섬으로부터 B섬, C섬에는 도달할 수 없기 때문에 연결되지 않은 것입니다.
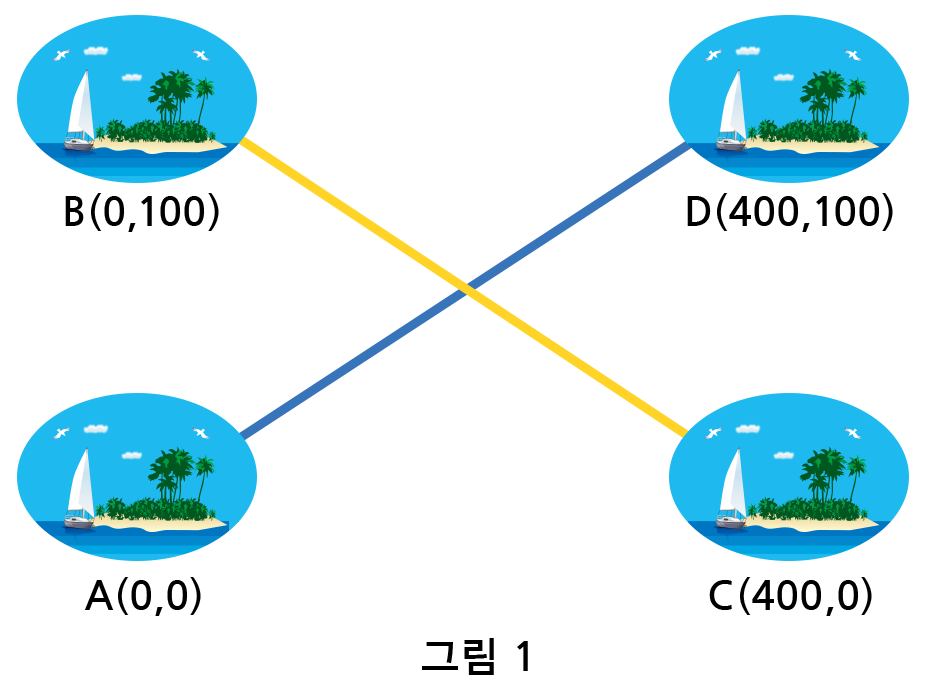
다음 두 가지의 경우는 모든 섬이 연결된 것입니다.

위와 같은 방법을 통해 인도네시아 내의 모든 섬들을 연결해야 하는 프로젝트입니다.
그림 3에서 B와 A처럼 직접적으로 연결된 경우도 있지만, B와 C처럼 여러 섬에 걸쳐 간접적으로 연결된 경우도 있습니다.
다만 인도네시아에서는 해저터널 건설로 인해 파괴되는 자연을 위해 다음과 같은 환경 부담금 정책이 있습니다.
- 환경 부담 세율(E)과 각 해저터널 길이(L)의 제곱의 곱(E * L^2)만큼 지불
총 환경 부담금을 최소로 지불하며, N개의 모든 섬을 연결할 수 있는 교통 시스템을 설계하시오.
위의 그림 2는 환경 부담금을 최소로 하며 모든 섬을 연결하고 있지만, 그림 3은 그렇지 않음을 알 수 있습니다.
💡 아이디어
문제를 딱 봤을 때 크루스칼 알고리즘을 이용하면 문제를 해결할 수 있을 것이라고 생각했다.
일단 Cost를 알아야 하기 때문에 모든 간선을 탐색하면서 Cost를 구한 뒤 Stack에 저장했다.
그 후에 이 Cost가 저장된 Stack을 오름차순으로 정렬한 뒤 가장 작은 Cost에 해당하는 간선부터 연결한다.
연결하기 전에 Union & Find를 통해 Cycle이 형성되지 않는지 확인한다.
그렇게 모든 간선이 이어지면 최소의 Cost로 모든 섬을 연결할 수 있다.
💡 소스코드
package SWEA;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.Collections;
import java.util.Stack;
import java.util.StringTokenizer;
class Graph implements Comparable<Graph> {
int x;
int y;
double cost = 0.0;
Graph(int x, int y, double cost) {
this.x = x;
this.y = y;
this.cost = cost;
}
//Collections.sort()를 사용하기 위함
@Override
public int compareTo(Graph o) {
if (this.cost < o.cost) {
return -1;
} else if (this.cost > o.cost) {
return 1;
}
return 0;
}
}
public class SWEA_P1251_하나로 {
static int N;// 섬의 개수
static double E;//세율
static Graph[] list;//입력을 받기위한 배열
static Stack<Graph> sorted;//두 정점과 cost를 저장하는 Stack
static int[] parent;//부모정보
static double SumCost;//cost의 합
public static void main(String[] args) throws Exception {
System.setIn(new FileInputStream("./SWEA_INPUT/SWEA_P1251_input.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer sz;
int T = Integer.parseInt(br.readLine());
for (int TC = 1; TC <= T; TC++) {
sz = new StringTokenizer(br.readLine());// N의 값
N = Integer.parseInt(sz.nextToken());
init();// x, y, cost 초기화
sz = new StringTokenizer(br.readLine());// x값 읽어오기
for (int i = 1; i <= N; i++)
list[i].x = Integer.parseInt(sz.nextToken());
sz = new StringTokenizer(br.readLine());// y값 읽어오기
for (int i = 1; i <= N; i++)
list[i].y = Integer.parseInt(sz.nextToken());
sz = new StringTokenizer(br.readLine());// E(세율)의 값
E = Double.parseDouble(sz.nextToken());
FindCost();
solve();
System.out.print("#" + TC + " ");
System.out.printf("%.0f\n", SumCost);
}
br.close();
}
//크루스칼 알고리즘
public static void solve() {
Collections.sort(sorted);
Collections.reverse(sorted);
while (!sorted.isEmpty()) {
Graph g = sorted.pop();
if(union(g.x, g.y))//두 정점의 부모가 다르면
SumCost += g.cost;//cost를 더해줌
}
}
public static boolean union(int x, int y) {
int parentX = FindParent(x);//x의 부모
int parentY = FindParent(y);//y의 부모
if(parentX == parentY)//같으면 false
return false;
else {//디르면
parent[parentY] = parentX;//y의 부모는 x의 부모
return true;
}
}
public static int FindParent(int v) {
if (parent[v] == v)
return v;
return FindParent(parent[v]);
}
//모든 간선의 cost를 Stack에 저장
public static void FindCost() {
for (int i = 1; i < N; i++) {
for (int j = i + 1; j <= N; j++) {
double cost = CostCalc(list[i].x, list[i].y, list[j].x, list[j].y);
sorted.push(new Graph(i, j, cost));
}
}
}
//cost를 계산하는 공식
public static double CostCalc(int x1, int y1, int x2, int y2) {
return E * Math.pow(Math.sqrt(Math.pow(x1 - x2, 2) + Math.pow(y1 - y2, 2)), 2);
}
//초기화
public static void init() {
list = new Graph[N + 1];
for (int i = 0; i <= N; i++)
list[i] = new Graph(0, 0, 0);
parent = new int[N + 1];
for (int i = 0; i <= N; i++)
parent[i] = i;
sorted = new Stack<Graph>();
SumCost = 0;
}
}💡 결과

MST(최소 신장 트리)와 관련된 문제는 거의 처음이지만 문제를 보자마자 최소 신장 트리로 접근해야 한다는 것은 알았다.
근데 Union & Find를 구현하는 것이 쉽게 생각나지 않아서 조금 애를 먹었다.
그래서 MST에 대해서는 나중에 다시 복습을 하고 글을 올릴 예정이다.
'Algorithm > SW Expert Academy' 카테고리의 다른 글
| [SWEA] #1861 - 정사각형 방 (0) | 2022.04.13 |
|---|---|
| [SWEA] #1267 - 작업순서 (0) | 2022.04.08 |
| [SWEA] #1249 - 보급로 (0) | 2022.04.05 |
| [SWEA] #1248 - 공통조상 (0) | 2022.03.29 |
| [SWEA] #1247 - 최적경로 (0) | 2022.03.23 |














