[SWEA] #1767 - 프로세서 연결하기

💡 출처
https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AV4suNtaXFEDFAUf
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
💡 문제
[설명]
삼성에서 개발한 최신 모바일 프로세서 멕시노스는 가로 N개 x 세로 N개의 cell로 구성되어 있다.

1개의 cell에는 1개의 Core 혹은 1개의 전선이 올 수 있다.

멕시노스의 가장자리에는 전원이 흐르고 있다.
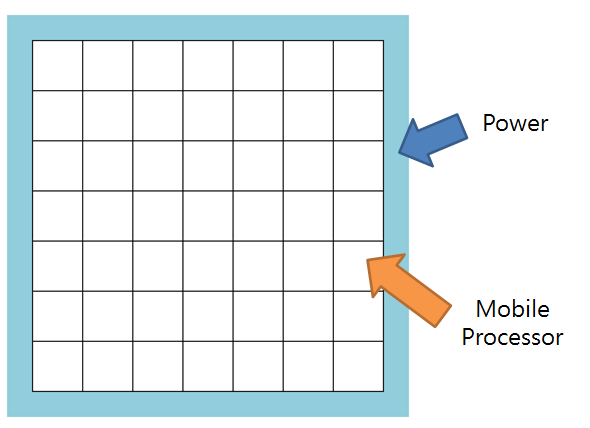
Core와 전원을 연결하는 전선은 직선으로만 설치가 가능하며,

전선은 절대로 교차해서는 안 된다.

초기 상태로는 아래와 같이 전선을 연결하기 전 상태의 멕시노스 정보가 주어진다.
(멕시노스의 가장자리에 위치한 Core는 이미 전원이 연결된 것으로 간주한다.)

최대한 많은 Core에 전원을 연결하였을 경우, 전선 길이의 합을 구하고자 한다.
단, 여러 방법이 있을 경우, 전선 길이의 합이 최소가 되는 값을 구하라.
[제약 사항]
1. 7 ≤ N ≤ 12
2. Core의 개수는 최소 1개 이상 12개 이하이다.
3. ⭐최대한 많은 Core에 전원을 연결해도, 전원이 연결되지 않는 Core가 존재할 수 있다.
💡 아이디어
큰 아이디어는 DFS를 이용한 완전 탐색이다.
가장자리의 Core는 전원이 연결된 상태이므로 무시하고, 가장자리에 있지 않은 Core들의 좌표를 우선 따로 저장한다.
그리고 저장해둔 Core의 좌표를 하나씩 꺼내 4방 탐색을 통해 전선을 연결할 수 있는 위치를 찾는다.
위치를 찾았다면 전선이 연결됐다는 표시로 CELL의 값을 2로 변경한다.
그리고 다음 Core좌표를 꺼내서 반복한다.
가장 중요한 것은 3번 제약사항이다.
만약 4방이 전부 막혀 전선을 연결할 수 없다면 그냥 다음 Core로 넘어가야 한다.
이런 식으로 한 바퀴를 돌면 전선을 연결한 코어의 개수, 전선 길이의 합을 구할 수 있다.
만약, 이전에 저장한 코어의 개수보다 많다면 코어의 개수, 전선 길이의 합을 갱신한다.
코어의 개수가 같다면 전선 길이의 합이 더 작은 것으로 값을 갱신한다.
💡 소스코드
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;
// Core의 좌표를 나타내는 class
class Core {
int row;
int col;
Core(int row, int col) {
this.row = row;
this.col = col;
}
}
public class SWEA_P_1767_프로세서_연결하기 {
static int N, maxcore, minsum; // N : 배열의 개수, maxcore : 최대 코어의 개수, minsum : 최소 전선의 합
static int[][] CELL; // CELL을 입력받는 배열
static ArrayList<Core> core; // Core의 좌표를 저장하는 ArrayList
static int[] dx = { -1, 1, 0, 0 }; // 상, 하, 좌, 우에 따른 행 값
static int[] dy = { 0, 0, -1, 1 }; // 상, 하, 좌, 우에 따른 열 값
public static void main(String[] args) throws Exception {
System.setIn(new FileInputStream("P1767_input.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer sz;
int T = Integer.parseInt(br.readLine());
// 입력 및 초기화
for (int TC = 1; TC <= T; TC++) {
N = Integer.parseInt(br.readLine());
CELL = new int[N + 1][N + 1];
core = new ArrayList<Core>();
for (int i = 1; i <= N; i++) {
sz = new StringTokenizer(br.readLine());
for (int j = 1; j <= N; j++) {
CELL[i][j] = Integer.parseInt(sz.nextToken());
if (CELL[i][j] == 1 && i != 1 && i != N && j != 1 && j != N)// 가장자리에 있는 Core가 아닌 Core이면
core.add(new Core(i, j)); // ArrayList에 추가
}
}
// 최대 코어의 개수, 최소 전선의 합 초기화
maxcore = Integer.MIN_VALUE;
minsum = Integer.MAX_VALUE;
// method 호출
solve(0, 0, 0);
System.out.println("#" + TC + " " + minsum);
}
br.close();
}
// DFS를 이용한 solution
public static void solve(int idx, int corenum, int sum) {
/* 종료 조건 */
// 만약 모든 코어를 확인했을 때
if (idx == core.size()) {
// 실제로 전원이 들어오는 core의 개수가 maxcore보다 많다면
if (corenum > maxcore) {
// 최대 코어의 개수와 최소 전선의 합 값을 갱신
maxcore = corenum;
minsum = sum;
}
// 전원이 들어오는 코어의 개수가 같을 경우
else if (corenum == maxcore)
minsum = Math.min(minsum, sum); // 최소 전선의 합으로 갱신
// 종료
return;
}
// ArrayList에서 코어의 좌표를 꺼냄
Core c = core.get(idx);
int row = c.row;
int col = c.col;
/*
* (1) 상, 하, 좌, 우 4방향을 탐색한다.
* (2) check(방향, 행, 열) method를 통해 전선을 연결할 수 있는지 확인한다.
* (3) 전선을 연결할 수 있다면 ArrayList의 다음 인덱스 번호, 코어의 개수 +1, sum에 전선의 길이를 합한 상태로 재귀 호출
* (4) 만약 4방향 모두 전선을 연결할 수 없다면 그냥 ArrayList의 인덱스 번호만 증가시키고 재귀 호출
*/
for (int i = 0; i < 4; i++) {// (1)
int len = check(i, row, col);// (2)
if (len != -1) {// (3)
visit(i, row, col);
solve(idx + 1, corenum + 1, sum + len);
unvisit(i, row, col);
}
// (4)
else if (len == -1 && i == 3)
solve(idx + 1, corenum, sum);
}
}
/*
* 전선을 연결할 수 있는지 check하는 method
* 전선을 연결할 수 있다면 그 길이를 반환
* 전선을 연결할 수 없다면 -1을 반환
* dir = 1 : 상
* dir = 2 : 하
* dir = 3 : 좌
* dir = 4 : 우
* x = 행, y = 열
*/
public static int check(int dir, int x, int y) {
switch (dir) {
case 0:
for (int i = 1; i < x; i++)
if (CELL[i][y] == 2 || CELL[i][y] == 1)
return -1;
return x - 1;
case 1:
for (int i = x + 1; i <= N; i++)
if (CELL[i][y] == 2 || CELL[i][y] == 1)
return -1;
return N - x;
case 2:
for (int i = 1; i < y; i++)
if (CELL[x][i] == 2 || CELL[x][i] == 1)
return -1;
return y - 1;
case 3:
for (int i = y + 1; i <= N; i++)
if (CELL[x][i] == 2 || CELL[x][i] == 1)
return -1;
return N - y;
}
return -1;
}
/*
* 방문한 곳은 2로 표시하는 method
* dir = 1 : 상
* dir = 2 : 하
* dir = 3 : 좌
* dir = 4 : 우
* x = 행, y = 열
*/
public static void visit(int dir, int x, int y) {
switch (dir) {
case 0:
for (int i = 1; i <= x; i++)
CELL[i][y] = 2;
break;
case 1:
for (int i = x; i <= N; i++)
CELL[i][y] = 2;
break;
case 2:
for (int i = 1; i <= y; i++)
CELL[x][i] = 2;
break;
case 3:
for (int i = y; i <= N; i++)
CELL[x][i] = 2;
break;
}
}
/*
* 방문했다고 표시한 곳을 다시 0으로 바꿔주는 method
* dir = 1 : 상
* dir = 2 : 하
* dir = 3 : 좌
* dir = 4 : 우
* x = 행, y = 열
*
*/
public static void unvisit(int dir, int x, int y) {
switch (dir) {
case 0:
for (int i = 1; i < x; i++)
CELL[i][y] = 0;
break;
case 1:
for (int i = x + 1; i <= N; i++)
CELL[i][y] = 0;
break;
case 2:
for (int i = 1; i < y; i++)
CELL[x][i] = 0;
break;
case 3:
for (int i = y + 1; i <= N; i++)
CELL[x][i] = 0;
break;
}
}
}💡 결과

SWEA 특유의 DFS를 이용한 완전 탐색 문제...
그냥 완전 탐색을 해도 되지만 조건이 까다롭고, 시간이 많이 걸려 시간 초과에 걸릴 수 있다.
그렇다고 DFS로 접근하기엔 생각을 떠올리기까지 꽤 많은 시간이 소요되는 문제ㅠㅠ...
이 문제 하나에 2시간 이상을 소모한 것 같다...
그래도 풀수록 빨라지는 것 같으니 비슷한 주제의 문제를 최대한 많이 풀어보도록 해야겠다.
'Algorithm > SW Expert Academy' 카테고리의 다른 글
| [SWEA] #1220 - Magnetic (0) | 2022.03.09 |
|---|---|
| [SWEA] #1219 - 길찾기 (0) | 2022.03.08 |
| [SWEA] #1218 - 괄호 짝짓기 (0) | 2022.03.07 |
| [SWEA] #1216 - 회문2 (0) | 2022.03.07 |
| [SWEA] #1260 - 화학물질2 (0) | 2022.03.02 |














