[SWEA] #1949 - 등산로 조성

💡 출처
https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AV5PoOKKAPIDFAUq
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
💡 문제
[설명]
등산로를 조성하려고 한다.
등산로를 만들기 위한 부지는 N * N 크기를 가지고 있으며, 이곳에 최대한 긴 등산로를 만들 계획이다.
등산로 부지는 아래 [Fig. 1]과 같이 숫자가 표시된 지도로 주어지며, 각 숫자는 지형의 높이를 나타낸다.
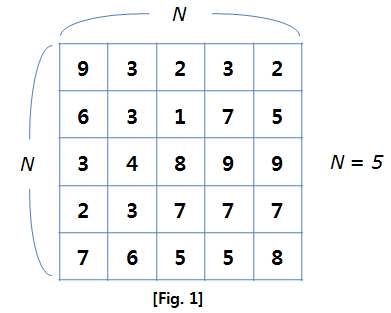
① 등산로는 가장 높은 봉우리에서 시작해야 한다.
② 등산로는 산으로 올라갈 수 있도록 반드시 높은 지형에서 낮은 지형으로 가로 또는 세로 방향으로 연결이 되어야 한다.
③ 긴 등산로를 만들기 위해 딱 한 곳을 정해서 최대 K 깊이만큼 지형을 깎는 공사를 할 수 있다.
N * N 크기의 지도가 주어지고, 최대 공사 가능 깊이 K가 주어진다.
이때 만들 수 있는 가장 긴 등산로를 찾아 그 길이를 출력하는 프로그램을 작성하라.
[제약 사항]
1. 지도의 한 변의 길이 N은 3 이상 8 이하의 정수이다. (3 ≤ N ≤ 8)
2. 최대 공사 가능 깊이 K는 1 이상 5 이하의 정수이다. (1 ≤ K ≤ 5)
3. 지도에 나타나는 지형의 높이는 1 이상 20 이하의 정수이다.
4. 지도에서 가장 높은 봉우리는 최대 5개이다.
5. 지형은 정수 단위로만 깎을 수 있다.
6. 필요한 경우 지형을 깎아 높이를 1보다 작게 만드는 것도 가능하다.
💡 아이디어
문제에서 지형의 높이를 최대 K값만큼 줄일 수 있다고 했으므로
2차원 배열 첫 번째 값을 1을 줄인 뒤에 4방 탐색을 통해 등산로의 길이를 구하고,
다음엔 2를 줄인 뒤에 4방 탐색을 통해 길이를 구하고, 그다음은 3, 4, ···, K까지 줄인 뒤에 길이를 구한다.
이 과정을 2차원 배열 모든 값에 대해 적용하면 완전 탐색을 통해 최대 길이를 구할 수 있다.
💡 소스코드
package SWEA;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class SWEA_P1949_등산로_조성 {
static int MAX_LEN = -1;
public static void main(String[] args) throws Exception {
System.setIn(new FileInputStream("./SWEA_INPUT/SWEA_P1949_input.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
for (int TC = 1; TC <= T; TC++) {
StringTokenizer sz = new StringTokenizer(br.readLine());
int N = Integer.parseInt(sz.nextToken());
int Depth = Integer.parseInt(sz.nextToken());
int MAX = -1;
MAX_LEN = -1;// 최대길이 초기화
// 시작 index를 저장하기 위한 ArrayList
ArrayList<Integer> startX = new ArrayList<Integer>();
ArrayList<Integer> startY = new ArrayList<Integer>();
int[][] array = new int[N][N];
// array에 값을 저장하면서 가장 높은 봉우리 찾기
for (int i = 0; i < N; i++) {
sz = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
array[i][j] = Integer.parseInt(sz.nextToken());
if (array[i][j] > MAX)
MAX = array[i][j];
}
}
// 가장 높은 봉우리를 찾아 시작점을 저장하는 ArrayList에 저장
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
if (array[i][j] == MAX) {
startX.add(i);
startY.add(j);
}
// Depth를 1만큼 줄여나가면서 완전탐색
for (int i = 0; i <= Depth; i++) {
for (int j = 0; j < N; j++) {
for (int k = 0; k < N; k++) {
if (array[j][k] - i < 0)
continue;
else
array[j][k] -= i;
for (int l = 0; l < startX.size(); l++) {
if (array[startX.get(l)][startY.get(l)] == MAX) {// Depth를 줄이면서 시작점이 아니게 된 곳은 무시
solve(array, startX.get(l), startY.get(l), 1);
}
}
array[j][k] += i;
}
}
}
System.out.println("#" + TC + " " + MAX_LEN);
}
br.close();
}
public static void solve(int[][] array, int i, int j, int cnt) {
int[] dx = { -1, 0, 1, 0 };
int[] dy = { 0, 1, 0, -1 };
// 상, 우, 하, 좌를 보면서 갈 길이 있으면 재귀호출
for (int k = 0; k < 4; k++) {
if (i + dx[k] > -1 && j + dy[k] > -1 && i + dx[k] < array.length && j + dy[k] < array.length) {
if (array[i][j] > array[i + dx[k]][j + dy[k]]) {
solve(array, i + dx[k], j + dy[k], cnt + 1);
}
}
}
MAX_LEN = Math.max(MAX_LEN, cnt);
}
}💡 결과

이 문제를 조금 더 효율적으로 풀어볼 방법은 없을까 고민을 했지만, 딱히 떠오르지 않았다.
그래서 완전 탐색으로 문제를 해결했는데 때로는 고민하는 시간에 완전 탐색을 구현하는 것이
문제를 푸는 시간을 단축시키는 것 같기도 하다....
'Algorithm > SW Expert Academy' 카테고리의 다른 글
| [SWEA] #2115 - 벌꿀채취 (0) | 2022.04.15 |
|---|---|
| [SWEA] #1952 - 수영장 (0) | 2022.04.15 |
| [SWEA] #1861 - 정사각형 방 (0) | 2022.04.13 |
| [SWEA] #1267 - 작업순서 (0) | 2022.04.08 |
| [SWEA] #1251 - 하나로 (0) | 2022.04.06 |














